{%- extends "base_math.xhtml" -%}
{%- block title -%}Number Wall Visualiser{%- endblock -%}
{%- block footer -%}{{ math_footer ("numberwall.xhtml") }}{%- endblock -%}
{%- block style %}
<link href="/css/numberwall.css" rel="stylesheet" />
<link href="/css/accordian.css" rel="stylesheet" />
{% endblock -%}
{%- block content %}
<h4>Number Wall Visualiser</h4>
<p>Git repository: <a href="/cgi-bin/cgit.cgi/number-wall">Link</a><br />
Mathologer video:
<a href="https://invidious.namazso.eu/watch?v=NO1_-qptr6c" class="external">Invidious</a>
<a href="https://www.youtube.com/watch?v=NO1_-qptr6c" class="external">Youtube</a></p>
<h5>9/11/2022</h5>
<h5>Overview</h5>
<p>On August 27, 2022, a youtube mathematician called the Mathologer published an interesting video
on the mathematical constructs known as number walls. In the description of that video he also
published a coding challenge of creating an implementation of the number wall algorithm.</p>
<p>This is not an entry into that coding challenge. This is just a tribute.</p>
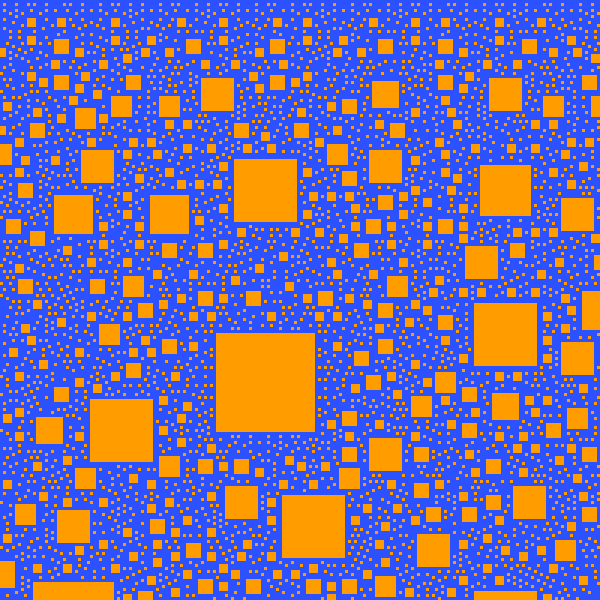
<p>For various reasons this didn't end up finished in the time period required, and in any case it
is not an online implementation and so doesn't qualify. But this project still has some fun tools to
play around with for anyone with an interest in math. Amongst other things, elaborate pictures of
the fractal square patterns produced by large number walls can be made.</p>
<div class="figure">
<img src="/img/pagoda_wall_mod_5.png"
alt="Number wall of the Pagoda sequence modulo 5"
height="600"
width="600" />
<div class="figcaption">Number wall of the <a href="https://oeis.org/A301849" class="external">
Pagoda sequence</a> with cells equal to 0 mod 5 in orange and others in blue</div>
</div>
<p>It is strongly recommended that you watch the Mathologer's video for an explanation of what
exactly a number wall is. If, for some reason, you don't want to do that or the video is
inaccessible, then the rules of how to construct a number wall are detailed in the appendix.</p>
<h5>Tools</h5>
<p>There are three programs provided:</p>
<ul>
<li><i>wallgen</i>, a command line program that generates a number wall from a given
input sequence in comma separated value format.</li>
<li><i>wallsolve</i>, a command line program that uses a number wall and polynomials constructed
from a given input sequence to find a recurrence relation that generates that sequence, and then
calculates the next integer using that recurrence relation.</li>
<li><i>visualwall</i>, a graphical program that creates a visual representation of a number wall
with cells equal to zero modulo a given number highlighted in one color, and all other cells
highlighted in a different color.</li>
</ul>
<p>An example of using <i>wallsolve</i> to calculate the next number in the sequence of integer
cubes:</p>
<div class="precontain">
<pre>
> wallsolve -i 1,8,27,64,125,216,343,512,729,1000
S(n) = 4S(n-1) - 6S(n-2) + 4S(n-3) - S(n-4)
Next: 1331
>
</pre>
</div>
<p>An example of <i>visualwall</i> has already been given in the overview in the form of the picture
of the Pagoda sequence number wall, and the output of <i>wallgen</i> is too verbose to show here.
</p>
<h5>Implementation Details</h5>
<p>All calculations to produce the number walls in these programs are done using the simple
construction rules in the appendix. No determinants were used, as that method would be more
computationally intensive.</p>
<p>Since the methods of constructing a number wall given by the Mathologer assume a sequence that is
infinite in both directions and any sequence used by these programs is finite, some compromises had
to be made. In particular, <i>visualwall</i> uses a longer sequence to generate its number wall and
then fits the largest square viewing area it can inside the resulting triangle of calculated values.
</p>
<p>The polynomial library made for <i>wallsolve</i> assumes that coefficients will always be
integers. This applies even to the division implementation, with only integer division being used
and the remainder term becoming larger than it may otherwise be expected to be if rationals were
permitted. As a number wall calculated from an integer sequence (or a sequence of polynomials with
integer coefficients) will always have integer values, this isn't actually a problem. But care had
to be taken in number wall construction so that division operations were always left until last.</p>
<p>The modulus values allowed by <i>visualwall</i> are not limited to prime numbers. If a composite
modulus is selected then the highlighted portions of cells equal to zero modulo that number may not
produce squares. The resulting pictures are, however, still interesting to examine.</p>
<p>At present <i>visualwall</i> only has the option to display either the Pagoda sequence or a
sequence of random numbers, unless a comma separated value formatted sequence is supplied in an
external file. It would not be hard for anyone with a passing knowledge of OCaml to add in different
sequences, but at this stage there is no need.</p>
<h5>Appendix: How to Construct a Number Wall</h5>
<p>A number wall is a grid of numbers that extends infinitely left, right, and down. It begins with
an infinite row of ones at the top, then below that a row containing the input sequence. All other
cells are computed according to the following rules.</p>
<div class="accordian">
<input type="checkbox" name="collapse" id="handle1" />
<label for="handle1">Toggle Cross Rule</label>
<div class="hidden_content">
<table class="rule">
<tr>
<th>Pattern</th>
<th>Relation</th>
<th>Notes</th>
</tr>
<tr>
<td>
<table class="wall">
<tr>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>a</mi>
</math>
</td>
<td> </td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>b</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>c</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>d</mi>
</math>
</td>
</tr>
<tr>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>e</mi>
</math>
</td>
<td> </td>
</tr>
</table>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>a</mi>
<mo>⁢</mo>
<mi>e</mi>
<mo>+</mo>
<mi>b</mi>
<mo>⁢</mo>
<mi>d</mi>
<mo>=</mo>
<msup>
<mi>c</mi>
<mn>2</mn>
</msup>
</mrow>
</math>
<br />
<br />
or alternatively
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>e</mi>
<mo>=</mo>
<mfrac>
<mrow>
<msup>
<mi>c</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mi>b</mi>
<mo>⁢</mo>
<mi>d</mi>
</mrow>
<mi>a</mi>
</mfrac>
</mrow>
</math>
<br />
<br />
where
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>a</mi>
<mo>≠</mo>
<mn>0</mn>
</mrow>
</math>
</td>
<td>
This rule is used to calculate the vast majority of cells.
</td>
</tr>
</table>
</div>
</div>
<div class="accordian">
<input type="checkbox" name="collapse" id="handle2" />
<label for="handle2">Toggle Long Cross Rule</label>
<div class="hidden_content">
<table class="rule">
<tr>
<th>Pattern</th>
<th>Relation</th>
<th>Notes</th>
</tr>
<tr>
<td>
<table class="wall">
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>a</mi>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>b</mi>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>c</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>d</mi>
</math>
</td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>e</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>f</mi>
</math>
</td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>g</mi>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>h</mi>
</math>
</td>
<td> </td>
<td> </td>
</tr>
</table>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
<mo>⁢</mo>
<mi>h</mi>
<mo>+</mo>
<mi>a</mi>
<mo>⁢</mo>
<msup>
<mi>g</mi>
<mn>2</mn>
</msup>
<mo>=</mo>
<msup>
<mi>d</mi>
<mn>2</mn>
</msup>
<mo>⁢</mo>
<mi>f</mi>
<mo>+</mo>
<mi>c</mi>
<mo>⁢</mo>
<msup>
<mi>e</mi>
<mn>2</mn>
</msup>
</mrow>
</math>
<br />
<br />
or alternatively
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>h</mi>
<mo>=</mo>
<mfrac>
<mrow>
<msup>
<mi>d</mi>
<mn>2</mn>
</msup>
<mo>⁢</mo>
<mi>f</mi>
<mo>+</mo>
<mi>c</mi>
<mo>⁢</mo>
<msup>
<mi>e</mi>
<mn>2</mn>
</msup>
<mo>-</mo>
<mi>a</mi>
<mo>⁢</mo>
<msup>
<mi>g</mi>
<mn>2</mn>
</msup>
</mrow>
<msup>
<mi>b</mi>
<mn>2</mn>
</msup>
</mfrac>
</mrow>
</math>
<br />
<br />
where
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>b</mi>
<mo>≠</mo>
<mn>0</mn>
</math>
</td>
<td>
If cell
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>a</mi>
</math>
goes out of bounds of the wall, it is considered equal to zero.
</td>
</tr>
</table>
</div>
</div>
<div class="accordian">
<input type="checkbox" name="collapse" id="handle3" />
<label for="handle3">Toggle Horseshoe Rule</label>
<div class="hidden_content">
<table class="rule">
<tr>
<th>Pattern</th>
<th>Relation</th>
<th>Notes</th>
</tr>
<tr>
<td>
<table class="wall">
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>a</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>b</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>c</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>d</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>e</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>f</mi>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>g</mi>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>h</mi>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>i</mi>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>j</mi>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>k</mi>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>l</mi>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>m</mi>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>n</mi>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>o</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>p</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>q</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>r</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>s</mi>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>t</mi>
</math>
</td>
</tr>
</table>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mfrac>
<mrow>
<mi>W</mi>
<mo>⁢</mo>
<mi>X</mi>
</mrow>
<mrow>
<mi>Y</mi>
<mo>⁢</mo>
<mi>Z</mi>
</mrow>
</mfrac>
<mo>=</mo>
<mi>S</mi>
</mrow>
</math>
where
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>W</mi>
</math>
is the common ratio of the arithmetic sequence
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>a</mi>
<mo>,</mo>
<mi>b</mi>
<mo>,</mo>
<mi>c</mi>
<mo>,</mo>
<mi>d</mi>
<mo>,</mo>
<mi>e</mi>
<mo>,</mo>
<mi>f</mi>
</mrow>
</math>
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>X</mi>
</math>
is the common ratio of the arithmetic sequence
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>t</mi>
<mo>,</mo>
<mi>s</mi>
<mo>,</mo>
<mi>r</mi>
<mo>,</mo>
<mi>q</mi>
<mo>,</mo>
<mi>p</mi>
<mo>,</mo>
<mi>o</mi>
</mrow>
</math>
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>Y</mi>
</math>
is the common ratio of the arithmetic sequence
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>a</mi>
<mo>,</mo>
<mi>g</mi>
<mo>,</mo>
<mi>i</mi>
<mo>,</mo>
<mi>k</mi>
<mo>,</mo>
<mi>m</mi>
<mo>,</mo>
<mi>o</mi>
</mrow>
</math>
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>Z</mi>
</math>
is the common ratio of the arithmetic sequence
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>t</mi>
<mo>,</mo>
<mi>n</mi>
<mo>,</mo>
<mi>l</mi>
<mo>,</mo>
<mi>j</mi>
<mo>,</mo>
<mi>h</mi>
<mo>,</mo>
<mi>f</mi>
</mrow>
</math>
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>S</mi>
</math>
is equal to
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mn>1</mn>
</math>
if the dimension of the zero square is even, or
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mn>-1</mn>
</math>
if the dimension is odd
</td>
<td>
All cells surrounding a square of zeros are guaranteed to be nonzero.<br />
<br />
This rule is applicable to squares of zeros of any finite size, but for the sake of
simplicity the previous rule should be used for isolated zeros.<br />
<br />
The cells that this rule should be targeted at calculating are those on the bottom row
below the square of zeros. Reformulating the math to solve for those cells is left as an
exercise to the reader.
</td>
</tr>
</table>
</div>
</div>
<div class="accordian">
<input type="checkbox" name="collapse" id="handle4" />
<label for="handle4">Toggle Broken Cross Rule</label>
<div class="hidden_content">
<table class="rule">
<tr>
<th>Pattern</th>
<th>Relation</th>
<th>Notes</th>
</tr>
<tr>
<td>
<table class="wall">
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>b</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>b</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>b</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>b</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>c</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>d</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>f</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>e</mi>
<mn>4</mn>
</msub>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>c</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>d</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>f</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>e</mi>
<mn>3</mn>
</msub>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>c</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>d</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>f</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>e</mi>
<mn>2</mn>
</msub>
</math>
</td>
</tr>
<tr>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>c</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>d</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>f</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>e</mi>
<mn>1</mn>
</msub>
</math>
</td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>h</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>h</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>h</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>h</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td> </td>
<td> </td>
</tr>
<tr>
<td> </td>
<td> </td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>g</mi>
<mn>4</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>g</mi>
<mn>3</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>g</mi>
<mn>2</mn>
</msub>
</math>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>g</mi>
<mn>1</mn>
</msub>
</math>
</td>
<td> </td>
<td> </td>
</tr>
</table>
</td>
<td>
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>Y</mi>
<mo>⁢</mo>
<mfrac>
<msub>
<mi>a</mi>
<mi>n</mi>
</msub>
<msub>
<mi>b</mi>
<mi>n</mi>
</msub>
</mfrac>
<mo>+</mo>
<mi>s</mi>
<mo>⁢</mo>
<mi>W</mi>
<mo>⁢</mo>
<mfrac>
<msub>
<mi>c</mi>
<mi>n</mi>
</msub>
<msub>
<mi>d</mi>
<mi>n</mi>
</msub>
</mfrac>
<mo>=</mo>
<mi>Z</mi>
<mo>⁢</mo>
<mfrac>
<msub>
<mi>g</mi>
<mi>n</mi>
</msub>
<msub>
<mi>h</mi>
<mi>n</mi>
</msub>
</mfrac>
<mo>+</mo>
<mi>s</mi>
<mo>⁢</mo>
<mi>X</mi>
<mo>⁢</mo>
<mfrac>
<msub>
<mi>e</mi>
<mi>n</mi>
</msub>
<msub>
<mi>f</mi>
<mi>n</mi>
</msub>
</mfrac>
</mrow>
</math>
<br />
<br />
where
<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mrow>
<mi>W</mi>
<mo>,</mo>
<mi>X</mi>
<mo>,</mo>
<mi>Y</mi>
<mo>,</mo>
<mi>Z</mi>
</mrow>
</math>
are the common ratios of the arithmetic sequences along the sides of the square of zeros
as in the Horseshoe Rule<br />
<br />
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>s</mi>
</math>
is equal to
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mn>-1</mn>
</math>
if
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>n</mi>
</math>
is odd and
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mn>1</mn>
</math>
if
<math xmlns="http://www.w3.org/1998/Math/MathML">
<mi>n</mi>
</math>
is even
</td>
<td>
As with the Horseshoe Rule, this rule is applicable to squares of zeros of any finite
size.<br />
<br />
The cells that this rule should be targeted at are those along the bottom denoted as
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>g</mi>
<mi>n</mi>
</msub>
</math>
but as with the previous rule, reformulating the math to solve for those cells is left
as an exercise to the reader.<br />
<br />
As with the Long Cross Rule, if any of the cells
<math xmlns="http://www.w3.org/1998/Math/MathML">
<msub>
<mi>a</mi>
<mi>n</mi>
</msub>
</math>
go out of bounds of the wall they are considered to be equal to zero. This can occur if
there are non-isolated zeros in the input sequence.
</td>
</tr>
</table>
</div>
</div>
<p>An example of a number wall:</p>
<table class="wall">
<tr>
<td>⋯</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>1</td>
<td>⋯</td>
</tr>
<tr>
<td>⋯</td>
<td>64</td>
<td>125</td>
<td>216</td>
<td>343</td>
<td>512</td>
<td>729</td>
<td>1000</td>
<td>⋯</td>
</tr>
<tr>
<td>⋯</td>
<td>721</td>
<td>1801</td>
<td>3781</td>
<td>7057</td>
<td>12097</td>
<td>19441</td>
<td>29701</td>
<td>⋯</td>
</tr>
<tr>
<td>⋯</td>
<td>2016</td>
<td>4140</td>
<td>7344</td>
<td>11844</td>
<td>17856</td>
<td>25596</td>
<td>35280</td>
<td>⋯</td>
</tr>
<tr>
<td>⋯</td>
<td>1296</td>
<td>1296</td>
<td>1296</td>
<td>1296</td>
<td>1296</td>
<td>1296</td>
<td>1296</td>
<td>⋯</td>
</tr>
<tr>
<td>⋯</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>0</td>
<td>⋯</td>
</tr>
<tr>
<td>⋰</td>
<td>⋮</td>
<td>⋮</td>
<td>⋮</td>
<td>⋮</td>
<td>⋮</td>
<td>⋮</td>
<td>⋮</td>
<td>⋱</td>
</tr>
</table>
<p>The above excerpt was taken from the number wall generated by the sequence of integer cubes. In
this case, the wall essentially ends in a row of all zeros as all subsequent rows below that will
also be zeros. Note however that this does not always happen.</p>
<p>A property of number walls is that zeros will always be arranged in squares. A singular isolated
zero is considered to be a 1x1 square and a wall ending in rows of zeros as above is considered to
be the start of a square of zeros of infinite size. This property can be used to supplement the
calculation rules.</p>
{% endblock -%}